12 Spring Constant Units Made Easy
Understanding the concept of spring constant units is crucial in the realm of physics, particularly in the study of simple harmonic motion and the behavior of springs under various forces. The spring constant, often denoted by the letter (k), is a measure of the stiffness of a spring. It represents the amount of force required to stretch or compress a spring by a unit distance. The unit of the spring constant is typically measured in Newtons per meter (N/m).
To delve into the specifics of spring constant units, let’s first explore what the spring constant represents. The spring constant is defined by Hooke’s Law, which states that the force (F) needed to extend or compress a spring by some distance (x) is proportional to that distance. Mathematically, this is expressed as (F = kx), where (k) is the spring constant. The value of (k) is dependent on the physical properties of the spring, such as its material and geometry.
Historical Evolution of Spring Constant Understanding
The concept of the spring constant has its roots in the work of Robert Hooke, an English natural philosopher and polymath, who in 1676 formulated his law regarding the behavior of springs. Hooke’s Law not only explained how springs behave under tension or compression but also laid the groundwork for understanding elastic materials and their properties. Over time, as physics evolved, so did our understanding of the spring constant and its role in describing the mechanical properties of materials and systems.
Technical Breakdown of Spring Constant Calculation
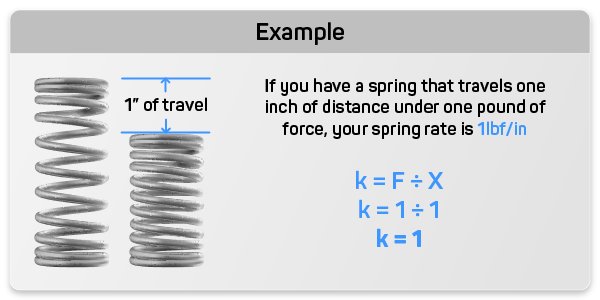
Calculating the spring constant of a spring involves understanding the relationship between the force applied to the spring and the resulting displacement. The formula (k = \frac{F}{x}) indicates that the spring constant is directly proportional to the force applied and inversely proportional to the displacement caused by that force. For instance, if a force of 10 N stretches a spring by 2 meters, the spring constant would be (k = \frac{10 \, \text{N}}{2 \, \text{m}} = 5 \, \text{N/m}).
Problem-Solution Framework: Common Challenges with Spring Constant Units
One common challenge in working with spring constant units is ensuring consistency in measurement units. When calculating the spring constant, it’s crucial that the force is measured in Newtons (N) and the displacement in meters (m), to obtain the spring constant in the correct units of N/m.
Solution: Always verify the units of measurement for force and displacement before calculating the spring constant. This ensures that the calculation yields a result in the appropriate units, facilitating accurate comparisons and further calculations.
Comparative Analysis: Different Springs and Their Spring Constants
Different springs have different spring constants, reflecting their varying stiffnesses. A spring with a high spring constant requires more force to stretch or compress it by a given distance than a spring with a low spring constant. For example:
- A stiff spring might have a spring constant of 100 N/m.
- A softer spring might have a spring constant of 20 N/m.
Understanding these differences is crucial in selecting the appropriate spring for specific applications, such as in mechanical devices, automotive suspensions, or even in biomedical devices.
Future Trends Projection: Advances in Spring Technology
As technology advances, so does the development of springs with tailored properties. Future trends may include the creation of springs with adjustable spring constants, allowing for real-time modification of stiffness based on application requirements. Additionally, the use of novel materials could lead to the development of springs with unprecedented strength-to-weight ratios, expanding their potential applications in fields like aerospace and robotics.
Decision Framework: Choosing the Right Spring Constant for an Application
When choosing a spring for a particular application, several factors must be considered, including the required spring constant, the maximum load, the operating environment (temperature, corrosion potential, etc.), and space constraints. A decision framework that weighs these factors can help in selecting the most appropriate spring for the task at hand.
- Define Requirements: Identify the necessary spring constant range and the maximum force the spring will need to withstand.
- Environmental Considerations: Consider how environmental factors might affect the spring’s performance and durability.
- Material Selection: Choose a material that meets the requirements for strength, corrosion resistance, and operational temperature range.
- Testing and Validation: Once a spring is selected, it should be tested under application-like conditions to validate its performance.
FAQ Section
What units are used to measure the spring constant?
+The spring constant is measured in units of force per unit distance, typically Newtons per meter (N/m).
How do you calculate the spring constant of a spring?
+The spring constant k can be calculated using the formula k = \frac{F}{x}, where F is the force applied to the spring, and x is the resulting displacement.
What factors affect the spring constant of a spring?
+The spring constant is affected by the physical properties of the spring, including its material and geometry. Different materials and designs can result in springs with a wide range of spring constants.
In conclusion, understanding the spring constant and its units is fundamental to working with springs in various applications. By recognizing the factors that influence the spring constant and how it is calculated, individuals can better design, select, and apply springs in their projects, whether in engineering, physics, or any other field where the behavior of elastic materials is critical. As technology advances, the development of springs with specific properties will continue to play a vital role in innovation and problem-solving across industries.


