Arcsin Integral Identity

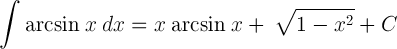
The arcsin integral identity is a fundamental concept in calculus, particularly in the realm of trigonometric integrals. This identity is crucial for evaluating definite integrals that involve the inverse sine function, denoted as arcsin(x) or sin^(-1)(x). The arcsin function returns the angle whose sine is a given number, and understanding its integral is vital for solving various problems in mathematics, physics, and engineering.

Introduction to Arcsin Integral

To delve into the arcsin integral identity, let’s first understand the basic properties of the arcsin function. The domain of arcsin(x) is [-1, 1], and its range is ([-\frac{\pi}{2}, \frac{\pi}{2}]). The derivative of arcsin(x) is given by (\frac{1}{\sqrt{1-x^2}}), which is a crucial piece of information for deriving the integral identity.

Derivation of Arcsin Integral Identity

The arcsin integral identity can be derived by considering the integral of (\frac{1}{\sqrt{1-x^2}}) with respect to x. This derivation involves recognizing that the derivative of arcsin(x) is (\frac{1}{\sqrt{1-x^2}}), implying that the integral of (\frac{1}{\sqrt{1-x^2}}) with respect to x is arcsin(x) plus a constant of integration.

Mathematically, this can be represented as: [ \int \frac{1}{\sqrt{1-x^2}} dx = \arcsin(x) + C ]

Where: - ( \int ) denotes the integral, - ( \frac{1}{\sqrt{1-x^2}} ) is the integrand, - ( dx ) indicates the variable of integration, - ( \arcsin(x) ) is the antiderivative (indefinite integral) of ( \frac{1}{\sqrt{1-x^2}} ), - ( C ) is the constant of integration.

Practical Applications

The arcsin integral identity has numerous practical applications in various fields. For instance, in physics, it is used to model the motion of objects under certain constraints, such as the simple pendulum. In engineering, it appears in the design of mechanisms and in the analysis of stress and strain in materials. Additionally, in computer science and graphics, the arcsin function is used in 3D modeling and animation to perform rotations and transformations.

Historical Context

The study of inverse trigonometric functions, including arcsin, dates back to ancient civilizations. However, the systematic development of these functions and their integrals occurred during the 17th and 18th centuries with the work of mathematicians like Isaac Newton and Leonhard Euler. They laid the foundation for the calculus of inverse functions, including the derivation of their integrals.

Advanced Topics and Extensions

For those interested in advanced topics, the arcsin integral identity is just the beginning. There are more complex integral identities involving combinations of trigonometric functions and their inverses. Additionally, the use of contour integration in complex analysis provides a powerful method for evaluating definite integrals involving arcsin and other inverse trigonometric functions.

Step-by-Step Problem Solving

To apply the arcsin integral identity in practice, follow these steps:

1. Identify the Integrand: Recognize when the integrand is in the form ( \frac{1}{\sqrt{1-x^2}} ) or a variation that can be transformed into this form.
2. Apply the Identity: Directly apply the arcsin integral identity to find the antiderivative.
3. Evaluate Definite Integrals: If evaluating a definite integral, apply the Fundamental Theorem of Calculus by substituting the limits of integration into the antiderivative and subtracting the results.
4. Consider Boundary Conditions: Ensure that the solution respects any given boundary conditions or constraints of the problem.

Example

Consider the integral ( \int_{0}^{1} \frac{1}{\sqrt{1-x^2}} dx ).

Using the arcsin integral identity: [ \int \frac{1}{\sqrt{1-x^2}} dx = \arcsin(x) + C ]

Applying the limits of integration: [ \int_{0}^{1} \frac{1}{\sqrt{1-x^2}} dx = \arcsin(1) - \arcsin(0) ] [ = \frac{\pi}{2} - 0 ] [ = \frac{\pi}{2} ]

Conclusion

In conclusion, the arcsin integral identity is a vital tool in the arsenal of calculus, enabling the efficient evaluation of integrals involving the inverse sine function. Its applications are diverse, ranging from fundamental problems in mathematics to practical challenges in physics, engineering, and computer science. By understanding and applying this identity, one can solve a wide range of problems with precision and clarity.