Sample Variance Shortcut Formula

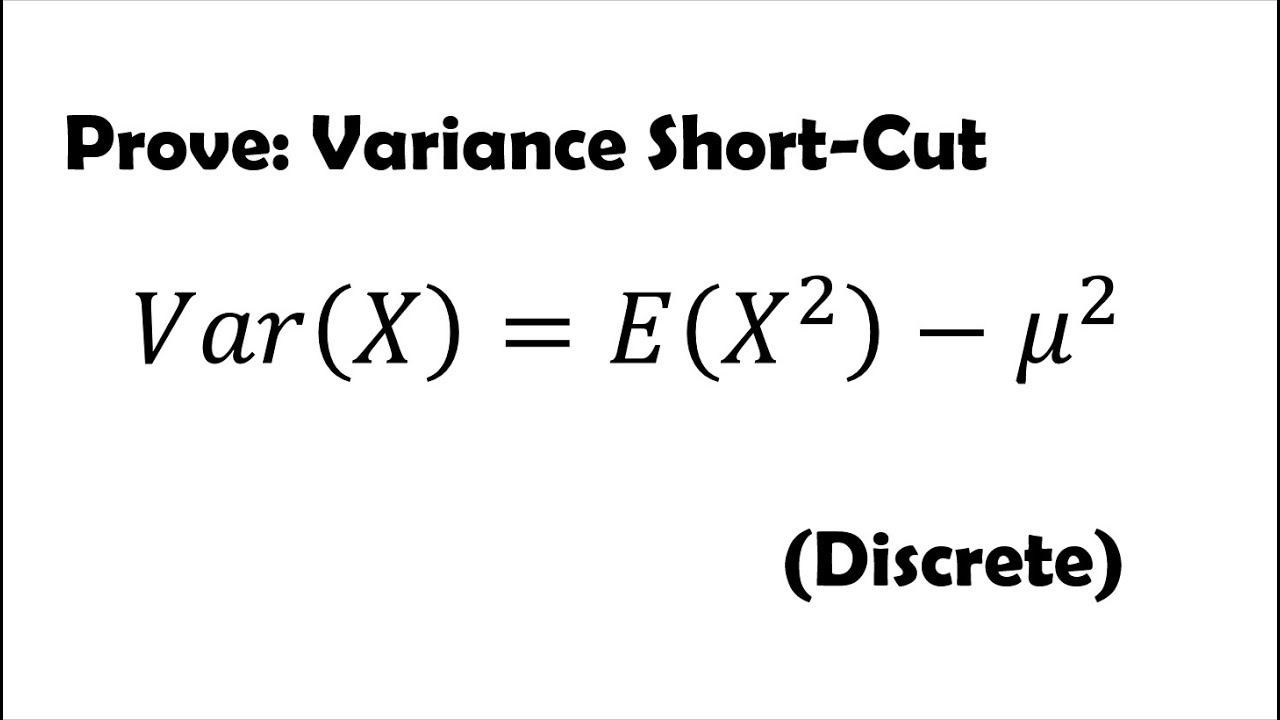
To apply a sample variance shortcut formula in statistical analysis, especially in the context of understanding and working with data, it’s essential to grasp the fundamental principles behind variance calculation. Variance is a measure of how much the numbers in a set spread out from their mean value. It’s a key concept in statistics and is used to understand the distribution of a dataset.

Understanding Variance

Variance is calculated as the average of the squared differences from the mean. For a dataset, the formula for variance (σ²) when the population is known is:

[ \sigma^2 = \frac{\sum_{i=1}^{N} (x_i - \mu)^2}{N} ]

Where: - (x_i) represents each individual data point, - (\mu) is the mean of the dataset, - (N) is the number of data points.

However, when dealing with a sample from a larger population, the formula for sample variance (s²) is slightly adjusted to:

[ s^2 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1} ]

Where: - (x_i) represents each data point in the sample, - (\bar{x}) is the mean of the sample, - (n) is the number of data points in the sample.

The adjustment from (N) to (n-1) is known as Bessel’s correction, which helps to make the sample variance a more unbiased estimator of the population variance.

Sample Variance Shortcut Formula

A shortcut formula for calculating sample variance involves first finding the mean of the dataset and then using the squared differences from this mean. The shortcut formula can be expressed as:

[ s^2 = \frac{\sum x_i^2 - \frac{(\sum x_i)^2}{n}}{n-1} ]

This formula simplifies the calculation by avoiding the need to individually subtract the mean from each data point before squaring. Instead, it uses the sums of the squares of the data points and the sum of the data points to find the variance in one step.

How to Apply the Formula

1. Sum of Squares: Calculate the sum of the squares of all data points ((\sum x_i^2)).
2. Sum of Data Points: Calculate the sum of all data points ((\sum x_i)).
3. Mean Calculation: Although not directly needed for the shortcut, ensure you have (n), the number of data points.
4. Apply the Shortcut Formula: Plug the values into the shortcut formula to find the sample variance.

Example

Suppose we have a sample dataset: 2, 4, 6, 8, 10.

1. Sum of Squares: (2^2 + 4^2 + 6^2 + 8^2 + 10^2 = 4 + 16 + 36 + 64 + 100 = 220)
2. Sum of Data Points: (2 + 4 + 6 + 8 + 10 = 30)
3. Number of Data Points: (n = 5)
4. Apply the Shortcut Formula: [ s^2 = \frac{220 - \frac{(30)^2}{5}}{5-1} ] [ s^2 = \frac{220 - \frac{900}{5}}{4} ] [ s^2 = \frac{220 - 180}{4} ] [ s^2 = \frac{40}{4} ] [ s^2 = 10 ]

Thus, the sample variance of the dataset is 10.

Conclusion

The sample variance shortcut formula provides an efficient method to calculate the spread of a dataset, essential in statistical analysis for understanding data dispersion. By following the steps outlined and applying the formula correctly, one can easily determine the variance of any given sample dataset.

In conclusion, understanding and applying the sample variance shortcut formula is crucial for efficient statistical analysis. It not only simplifies the calculation process but also provides a reliable method for estimating the spread of a dataset, facilitating deeper insights into the data’s characteristics.