What Are The Different Mathematical Properties
Mathematics is a vast and intricate field, encompassing a wide range of concepts, theories, and properties. At its core, mathematics is concerned with the study of numbers, quantities, and shapes, as well as the relationships between them. One of the fundamental aspects of mathematics is the concept of mathematical properties, which are attributes or characteristics that describe the behavior of mathematical objects, such as numbers, functions, and geometric shapes.
In this article, we will delve into the different mathematical properties, exploring their definitions, examples, and significance in various mathematical contexts. We will also examine how these properties are used to describe and analyze mathematical objects, and how they are applied in real-world problems and applications.
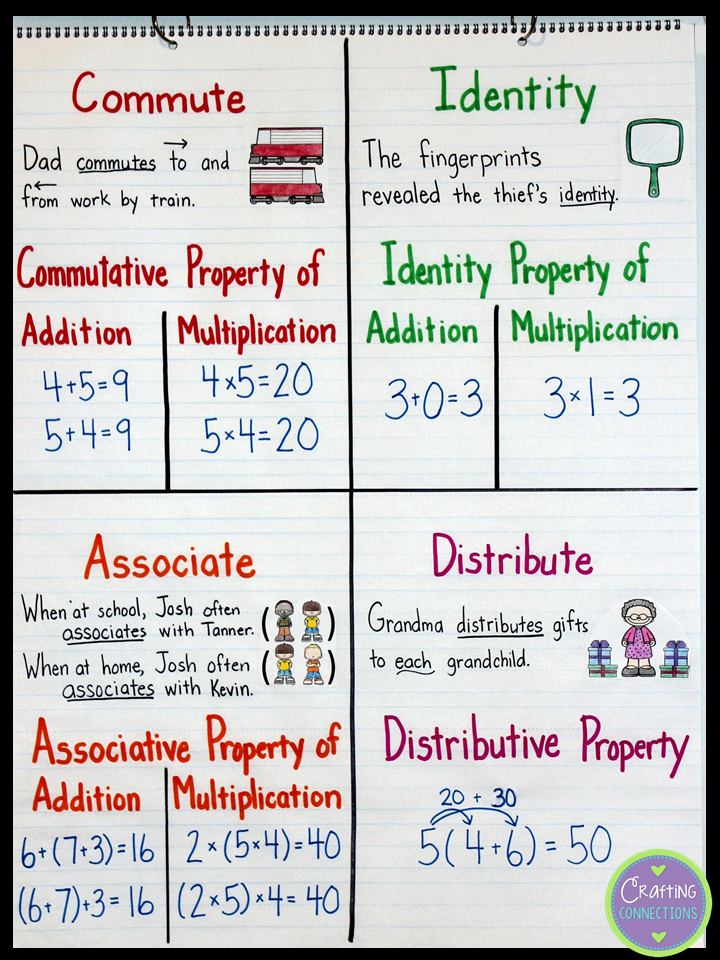
Commutative Property
The commutative property is a fundamental concept in mathematics, stating that the order of two or more numbers being added or multiplied does not affect the result. For example, in the expression a + b, the commutative property asserts that a + b = b + a. This property is essential in various mathematical operations, including addition, multiplication, and matrix algebra.
To illustrate the commutative property, consider the following example: 2 + 3 = 3 + 2 = 5. In this example, the order of the numbers being added does not change the result, demonstrating the commutative property of addition.
Associative Property
The associative property is another crucial concept in mathematics, which states that the order in which we perform operations on three or more numbers does not affect the result. For instance, in the expression (a + b) + c, the associative property asserts that (a + b) + c = a + (b + c). This property is vital in various mathematical operations, including addition, multiplication, and exponentiation.
To illustrate the associative property, consider the following example: (2 + 3) + 4 = 2 + (3 + 4) = 9. In this example, the order in which we perform the addition operations does not change the result, demonstrating the associative property of addition.
Distributive Property
The distributive property is a mathematical concept that describes the relationship between addition and multiplication. It states that a single operation (either addition or multiplication) can be distributed over another operation. For example, in the expression a(b + c), the distributive property asserts that a(b + c) = ab + ac. This property is essential in various mathematical operations, including algebra, geometry, and calculus.
To illustrate the distributive property, consider the following example: 2(3 + 4) = 2(3) + 2(4) = 6 + 8 = 14. In this example, the distributive property allows us to distribute the multiplication operation over the addition operation, demonstrating its significance in mathematical calculations.
Identity Property
The identity property is a mathematical concept that describes the existence of an identity element in a set of numbers. It states that there exists an element, called the identity element, which does not change the result when combined with any other element in the set. For example, in the expression a \cdot 1 = a, the identity property asserts that the number 1 is the identity element for multiplication.
To illustrate the identity property, consider the following example: 2 \cdot 1 = 2. In this example, the number 1 does not change the result when multiplied by 2, demonstrating the identity property of multiplication.
Inverse Property
The inverse property is a mathematical concept that describes the existence of an inverse element in a set of numbers. It states that for each element in the set, there exists an inverse element, which, when combined with the original element, results in the identity element. For example, in the expression a \cdot a^{-1} = 1, the inverse property asserts that a^{-1} is the inverse element of a.
To illustrate the inverse property, consider the following example: 2 \cdot \frac{1}{2} = 1. In this example, the number \frac{1}{2} is the inverse element of 2, demonstrating the inverse property of multiplication.
Symmetric Property
The symmetric property is a mathematical concept that describes the relationship between two or more elements in a set. It states that if a is related to b, then b is also related to a. For example, in the expression a = b, the symmetric property asserts that if a is equal to b, then b is also equal to a.
To illustrate the symmetric property, consider the following example: 2 = 2. In this example, the number 2 is equal to itself, demonstrating the symmetric property of equality.
Transitive Property
The transitive property is a mathematical concept that describes the relationship between three or more elements in a set. It states that if a is related to b and b is related to c, then a is also related to c. For example, in the expression a = b and b = c, the transitive property asserts that a = c.
To illustrate the transitive property, consider the following example: 2 = 3 - 1 and 3 - 1 = 2. In this example, the number 2 is equal to 3 - 1, and 3 - 1 is equal to 2, demonstrating the transitive property of equality.
Reflexive Property
The reflexive property is a mathematical concept that describes the relationship between an element and itself in a set. It states that every element is related to itself. For example, in the expression a = a, the reflexive property asserts that every element is equal to itself.
To illustrate the reflexive property, consider the following example: 2 = 2. In this example, the number 2 is equal to itself, demonstrating the reflexive property of equality.
Additive Inverse Property
The additive inverse property is a mathematical concept that describes the existence of an additive inverse element in a set of numbers. It states that for each element in the set, there exists an additive inverse element, which, when added to the original element, results in the additive identity element (usually 0). For example, in the expression a + (-a) = 0, the additive inverse property asserts that -a is the additive inverse element of a.
To illustrate the additive inverse property, consider the following example: 2 + (-2) = 0. In this example, the number -2 is the additive inverse element of 2, demonstrating the additive inverse property of addition.
Multiplicative Inverse Property
The multiplicative inverse property is a mathematical concept that describes the existence of a multiplicative inverse element in a set of numbers. It states that for each element in the set, there exists a multiplicative inverse element, which, when multiplied by the original element, results in the multiplicative identity element (usually 1). For example, in the expression a \cdot a^{-1} = 1, the multiplicative inverse property asserts that a^{-1} is the multiplicative inverse element of a.
To illustrate the multiplicative inverse property, consider the following example: 2 \cdot \frac{1}{2} = 1. In this example, the number \frac{1}{2} is the multiplicative inverse element of 2, demonstrating the multiplicative inverse property of multiplication.
In conclusion, mathematical properties are essential concepts in mathematics, describing the behavior of mathematical objects and the relationships between them. By understanding these properties, we can better analyze and solve mathematical problems, and develop a deeper appreciation for the beauty and complexity of mathematics.
What is the difference between the commutative and associative properties?
+The commutative property states that the order of two or more numbers being added or multiplied does not affect the result, whereas the associative property states that the order in which we perform operations on three or more numbers does not affect the result.
What is the significance of the distributive property in mathematics?
+The distributive property is essential in various mathematical operations, including algebra, geometry, and calculus, as it describes the relationship between addition and multiplication.
What is the difference between the identity and inverse properties?
+The identity property describes the existence of an identity element in a set of numbers, whereas the inverse property describes the existence of an inverse element in a set of numbers.
By understanding the different mathematical properties, we can develop a deeper appreciation for the beauty and complexity of mathematics, and improve our ability to analyze and solve mathematical problems. Whether you are a student, teacher, or simply a mathematics enthusiast, recognizing and applying these properties can help you unlock the secrets of mathematics and discover new insights and perspectives.